Daniel Liu
May, 2021
Introduction
When we think of the word equation, we often think of quadratics and polynomials where the solutions are complex expressions involving square roots and  . However, diophantine equations completely revise the above connotations that associate with the equal sign: they only involve integer solutions. This means that when looking at a diophantine equation, for example
. However, diophantine equations completely revise the above connotations that associate with the equal sign: they only involve integer solutions. This means that when looking at a diophantine equation, for example  , would not be part of the solution set. In this guide, we will explore how to solve diophantine equations, their general solution forms, and their applications in the field of number theory.
, would not be part of the solution set. In this guide, we will explore how to solve diophantine equations, their general solution forms, and their applications in the field of number theory.
Solving 2-Variable Diophantine Equations
Consider the equation  . Typically when solving, we would simply set
. Typically when solving, we would simply set  equal to
equal to  and graph the equation on a Cartesian plane. However, things get interesting when we only think about the integer solutions.
and graph the equation on a Cartesian plane. However, things get interesting when we only think about the integer solutions.
Geometrically speaking, the solution set would look like a group of individual, collinear points on a graph that can all be represented by integer coordinates. In fact, there are an infinite number of said points, and thus an infinite number of solutions.
Remark: A diophantine equation has an infinite number of solutions.
Now that we understand what a typical set of solutions to a 2-variable diophantine equation would look like, we get right into solving them.
The general protocols that one follows when solving these equations using the format  are:
are:
- Set
 .
. - Find an integer pair
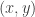 that satisfies the above equation.
that satisfies the above equation. - Turn the equation into
 by multiplying
by multiplying  and
and  by
by  .
. - Use the above solution pair to find a general form for the equation’s solutions.
Needless to say, the four steps detailed above make very little sense without application. We will now look at some examples to develop better intuition for diophantine equations.
Example 1.1: Solve the diophantine equation 
We start off with an easy equation; step one of the above procedure has already been satisfied. Now, as per step 2, we find one solution. It is fairly obvious that we have a solution at 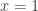 and
and 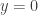 . But is this the only solution?
. But is this the only solution?
There’s no need to worry about step 3 since 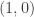 is already a solution to the original equation (more on that in later problems). Looking at step 4, we are asked to find a general form for all solutions of the equation, meaning that the equation has more than one solution (an infinite amount to be exact, as noted previously).
is already a solution to the original equation (more on that in later problems). Looking at step 4, we are asked to find a general form for all solutions of the equation, meaning that the equation has more than one solution (an infinite amount to be exact, as noted previously).
So what’s another solution? Playing around with numbers a bit, we come to the conclusion that  is also a solution. What about
is also a solution. What about  ? Plugging the numbers in, we see that it is indeed valid. Now some may see a pattern at this point; can you name it?
? Plugging the numbers in, we see that it is indeed valid. Now some may see a pattern at this point; can you name it?
The pattern here is that each new solution can be found by adding 1 to the  value and subtracting 1 from the
value and subtracting 1 from the  value of the preceding solution pair. Hence, we have
value of the preceding solution pair. Hence, we have  derived from adding 1 to 1 and subtracting 1 from 0 in the solution pair
derived from adding 1 to 1 and subtracting 1 from 0 in the solution pair 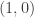 .
.
Thus far, we’ve exhibited this pattern for positive  -values. Naturally, this raises the question- does this pattern work for negative
-values. Naturally, this raises the question- does this pattern work for negative  -values as well? Well let’s test some values.
-values as well? Well let’s test some values.
Remark: When unsure if a pattern holds under particular conditions, it is always a good idea to make sure by testing values.
We find a “base case” involving a negative  -value to build off of by guess and check.
-value to build off of by guess and check.  is the solution pair with the largest
is the solution pair with the largest  -value that is still negative, so we can use it as our base.
-value that is still negative, so we can use it as our base.
Applying our previously found rule of adding to the  -value and subtracting from the
-value and subtracting from the  -value, we can quickly see that
-value, we can quickly see that  simply gets larger and larger until it becomes positive. Clearly, the above rule is quite useless. Does this mean the pattern we found is invalid for all negative
simply gets larger and larger until it becomes positive. Clearly, the above rule is quite useless. Does this mean the pattern we found is invalid for all negative  ? Not necessarily.
? Not necessarily.
If you’ve been reading closely, you may have already found the problem with our rule: It was formed under the pretense that  gets bigger and bigger and that
gets bigger and bigger and that  gets smaller and smaller. Therefore, we cannot use it to verify a case in which
gets smaller and smaller. Therefore, we cannot use it to verify a case in which  is set to continuously decrease.
is set to continuously decrease.
How can we transform it to encompass the fact that  decreases from our base case? One idea is to reverse our rule; that is, instead of having
decreases from our base case? One idea is to reverse our rule; that is, instead of having  increase by
increase by  and
and  decreases by
decreases by  each time, we have
each time, we have  decrease by
decrease by  and
and  increase by
increase by  .
.
Does it work? Well the best thing to do here is to test cases. We started off with  . Now, we test
. Now, we test 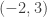 . Plugging these values in, it is easy to see that the original equation holds. What about
. Plugging these values in, it is easy to see that the original equation holds. What about  ? Again, it works. From here, further testing of values shows that this new rule over the domain of negative integers holds.
? Again, it works. From here, further testing of values shows that this new rule over the domain of negative integers holds.
We’ve found a pattern now -two actually- for both positive and negative integers. Back to step 4; how do we write these patterns algebraically? More importantly, how do we summarize them as one form? For now, let’s just worry about the first pattern. It can be summarized as  . This is true because, instead of comparing the case at hand to the previous case, we can compare the case at hand to the base case itself. That is, instead of comparing
. This is true because, instead of comparing the case at hand to the previous case, we can compare the case at hand to the base case itself. That is, instead of comparing  to
to  , we compare
, we compare  to our base case
to our base case 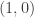 . From here we see that each time some integer
. From here we see that each time some integer  is added to the
is added to the  value, that same integer
value, that same integer  is subtracted from the
is subtracted from the  value. Now what about the negative case?
value. Now what about the negative case?
Here’s the part where we are saved by a bout of clever algebra:  includes all solutions involving a negative
includes all solutions involving a negative  because
because  doesn’t have to be positive. If
doesn’t have to be positive. If  is negative, it would imply the exact same rule that our rule for negative
is negative, it would imply the exact same rule that our rule for negative  ’s establishes. Thus, we have found the solution to the diophantine equation
’s establishes. Thus, we have found the solution to the diophantine equation  .
.
Example 1.2: Solve the diophantine equation  .
.
Now that we have a better understanding of the basics of solving these equations, we jump right to a typical problem.
By step 1, we set  .
.
Following step 2, we guess and check to find a solution for this case to use it as our base;  works.
works.
From here, we multiply the solution pair by 13 to get  as step 3 instructs. Before moving on, we check to see if it still satisfies the equation:
as step 3 instructs. Before moving on, we check to see if it still satisfies the equation:  . It is valid.
. It is valid.
We now begin step 4. For ease of computation, we can refer to the equation  to find solutions and multiply them by
to find solutions and multiply them by 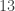 to satisfy our original equation. Aside from
to satisfy our original equation. Aside from  ,
,  works as well after some guess-and-check. But wait.
works as well after some guess-and-check. But wait.
We notice the difference between the  -coordinates of the two solutions is
-coordinates of the two solutions is 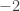 , and the difference between the
, and the difference between the  -coordinates is
-coordinates is 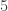 . Is this a coincidence? Our intuition gained from the previous problem tells us it might not be. But let’s test just to make sure.
. Is this a coincidence? Our intuition gained from the previous problem tells us it might not be. But let’s test just to make sure.
 seems to work. And so does
seems to work. And so does  .
.
The pattern does hold. And as the previous problem told us, the pattern will continue to hold regardless of positive or negative  -values.
-values.
But what happens when we multiply everything by 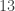 ? When we multiply
? When we multiply  and
and  each by 13, the difference in
each by 13, the difference in  -coordinates is now
-coordinates is now  and the difference in
and the difference in  -coordinates is now
-coordinates is now  .
.
So is this the new rule, differing by  and
and  , or does the old rule of
, or does the old rule of 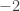 and
and 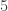 still hold?
still hold?
Let’s investigate. Our original case is now  , and
, and  becomes
becomes  . To get to
. To get to  , we now subtract
, we now subtract  from the
from the  -coordinate and add
-coordinate and add  to the
to the  -coordinate. What if we simply subtract
-coordinate. What if we simply subtract  from the
from the  -coordinate and add
-coordinate and add 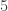 to the
to the  -coordinate? We then end up with
-coordinate? We then end up with  . Turns out, this still works!
. Turns out, this still works!
Thus we have a general solution now:  .
.
Exercise 1.1: Solve the diophantine equation  .
.
Exercise 1.2: Solve the diophantine equation  .
.
Exercise 1.3: Solve the diophantine equation  .
.
A Simplification
By now, you may be wondering why solving diophantine equations can be so tedious. Although it only technically involves 4 steps, step 4 is long and computation-heavy; easy to make errors on. So then the question becomes, is there an easier way?
The answer comes in the form of a theorem:
If  and
and  are relatively prime and
are relatively prime and  is a base case of the equation, then the diophantine equation
is a base case of the equation, then the diophantine equation  is given by
is given by

for some, not necessarily positive integer  .
.
The proof of this theorem is actually a relatively simple one: We simply need to prove that  . This is true because, since
. This is true because, since  is already equal to
is already equal to  , we can set the two equal to each other to prove that
, we can set the two equal to each other to prove that  equals
equals  as well. The remainder of this proof will not be fully detailed for the sake of brevity, but direct expansion and cancellation of terms on the right hand side can easily verify this.
as well. The remainder of this proof will not be fully detailed for the sake of brevity, but direct expansion and cancellation of terms on the right hand side can easily verify this.
Theorem Application
We now know a much simpler way to solve diophantine equations. However, our understanding of this concept is still reasonably shallow.
Example 2.1: Solve the diophantine equation  .
.
This example will be a continuation of example 1.2. This time, we will instead use the theorem to solve it.
As found in 1.2, our base case is  . Directly using our theorem and substituting in values, our general solution is
. Directly using our theorem and substituting in values, our general solution is  , which, because
, which, because  can be positive or negative, is the same thing as
can be positive or negative, is the same thing as  .
.
Needless to say, this theorem vastly simplifies our original 4-step process, though still retaining its structure.
Remark: This is a great example of how theorems can be useful, time-saving tools in mathematics.
Exercise 2.1: Solve the diophantine equation  (using the theorem).
(using the theorem).
Exercise 2.2: Solve the diophantine equation  (using the theorem).
(using the theorem).
Exercise 2.3: Solve the diophantine equation  (using the theorem).
(using the theorem).
Exercise 2.4: Two farmers agree that pigs are worth 300 dollars and that goats are worth 210 dollars. When one farmer owes the other money, he pays the debt in pigs or goats, with “change” received in the form of goats or pigs as necessary. (For example, a 390 dollar debt could be paid with two pigs, with one goat received in change.) What is the amount of the smallest positive debt that can be resolved in this way (2006 AMC 12A Problem 14).
A More Complex Method
Now what if, instead of an easy base case, we get something like  ? We can’t really guess-and-check our way out of this one.
? We can’t really guess-and-check our way out of this one.
The procedure for these “complex” diophantine equations is outlined as follows:
- Create two separate equations, one involving
 , and another involving
, and another involving 
- Solve the equations using algebra to obtain a general form with no explicit base solution.
- Use the Euclidean algorithm to obtain a base solution.
As we have done previously, we will now use  as an example to gain intuition on the 3-step process above.
as an example to gain intuition on the 3-step process above.
Step one: creating two separate equations.
– 
– 
That’s all there is to it.
Step two: solving the equations for a non-specified base solution.
Subtract the equations to obtain:

Move one term to the other side:

Use algebraic manipulations on the right hand side:

From here, observe that, since 79 and 243 are relatively prime,
 and
and 
This implies that
 and
and 
Thus, we have the solution  . But to complete the problem, we must find an
. But to complete the problem, we must find an 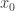 and an
and an  . This is where the hard part comes in.
. This is where the hard part comes in.
We apply the Euclidean algorithm repeatedly to get:


But then we must reverse this process:



Thus, the general form of the solution is  .
.
However, note that this problem is a particularly easy one due to the fact that the Euclidean algorithm portion was not very extensive. Other “complex” diophantine equations will have far more computation involved.
This way of solving diophantine equations can be confusing and tedious, and is generally not recommended unless guess-and-check is completely out of the question.
Exercise 1.1: Solve the diophantine equation  .
.
Exercise 1.2: Solve the diophantine equation  .
.
. Thus,
is simply 2, since the numbers less than 3 that are relatively prime to 3 are 1 and 2. Similarly,
is 4, as we see there are four integers less than 8 relatively prime to 8: 1, 3, 5, and 7. As you will see later, this function is extremely useful in number theory, especially when computing the last a digits of a given expression, such as
. Note that Euler’s totient is synonymous with the phi function and both names will be used interchangeably throughout this guide.
of a prime p is always p-1.
. This renders it useless for numbers such as 35 (
) whose factorizations involve more than one prime.
.
, we simply plug this value into the formula to get
.
. We repeat the above process to compute that
is equal to 2. Because 3, 7, and 23 are all prime, we can use the identity that ϕ of a prime number is equivalent to the prime number minus one:
,
,
. To finish out the problem, we multiply together the values of each computation to get 528.
.
.
.
.
by Euler’s theorem.
, which mean
is 40. Thus,
. Further,
. This means that
.
. From here,
. Therefore, the last two digits of
are 69.
.
. Moreover, if
, then
by the property
.
. If we can do this, we know
, based on the claim above. Since 4 and 25 are relatively prime,
. Because
is equivalent to
,
. We can easily compute
by hand to get that
.
. For the sake of brevity, its calculation will not be fully explained, since it is a direct application of Euler’s theorem and exactly mirrors example 2.1, but with different numbers.
.
, which equals
. Since -300 is the closest multiple of 100 to -244 that is still less than -244, we perform
to arrive at our answer, 56.
.
, where there are 2021 7’s in the tower. Hint: A(N) is equivalent to N (mod 9).
. Hint: Consider an arbitrary set A whose elements are all taken modulo m, where each element is relatively prime to m. Prove that A is identical to set B mod m, where the elements of B are found by multiplying the elements of A by a constant a.

